Il existe, dans la nature, des phénomènes que nous pouvons décrire avec une telle précision qu’il est possible de prédire leur comportement futur sur de très longues périodes temporelles. Cependant, certaines dynamiques, comme celle décrite par la théorie darwinienne de l’évolution, sont imprévisibles.
Si la prédiction mathématique devient impossible, que peut-on dire d’un phénomène qui, par nature, n’est pas prédictible ?

Fig.1 Illustration d’un exemple de principe d‘évolution.
Dans cet article, nous parlerons de « l’évolution ouverte » (EO). Il s’agit d’un processus de création de nouveautés typique des systèmes vivants, tel que l’a décrit le naturaliste Charles Darwin dans la deuxième partie du XIXe siècle.
L’évolution darwinienne repose sur le principe de la génération de nouvelles espèces vivantes. Cela se fait à travers l’itération des phénomènes de variation, de reproduction et de sélection.
Nous verrons non seulement qu’elle représente un domaine de recherche de pointe en biologie théorique et en physique théorique. Elle a aussi des répercussions importantes dans l’étude des systèmes complexes. Enfin, elle influence un bon nombre d’applications technologiques.
Nouveautés et créativité
La dynamique de la majorité des phénomènes naturels connus est, par nature, prévisible grâce à des méthodes mathématiques. Ces dernières ne sont, cependant, pas suffisantes pour prédire les comportements de certains systèmes vivants qui se distinguent des systèmes inanimés par leur forte dépendance à leur histoire ; résultat de l’ensemble des choix de l’individu et de son groupe social.
Variation comme changement du changement
Cette historicité explique l’impossibilité de prédire les changements avec les outils mathématiques actuels. En effet, l’enchaînement d’événements rend les propriétés de deux systèmes vivants, initialement identiques, singulières.
Par exemple, les événements vécus dans la vie de deux personnes jumelles feront d’elles deux individus foncièrement différents, bien qu’aucune différence physique ne les distinguait à la naissance. Darwin parlerait ici d’adaptation.
En physique, on étudie des objets appelés *génériques* [1], car les lois qui les régissent restent invariées tout au long de leur histoire. En biologie, en revanche, on parle d’objets *spécifiques* [1], car leur détermination dépend de manière spécifique de leur histoire.
On peut redéfinir l’EO comme un processus d’apparition de nouveautés jouant un rôle a priori imprévisible. Il s’agit ici d’innovations fonctionnelles. Ces innovations modifient de manière irréversible les fonctions du système et, par conséquent, ses lois.
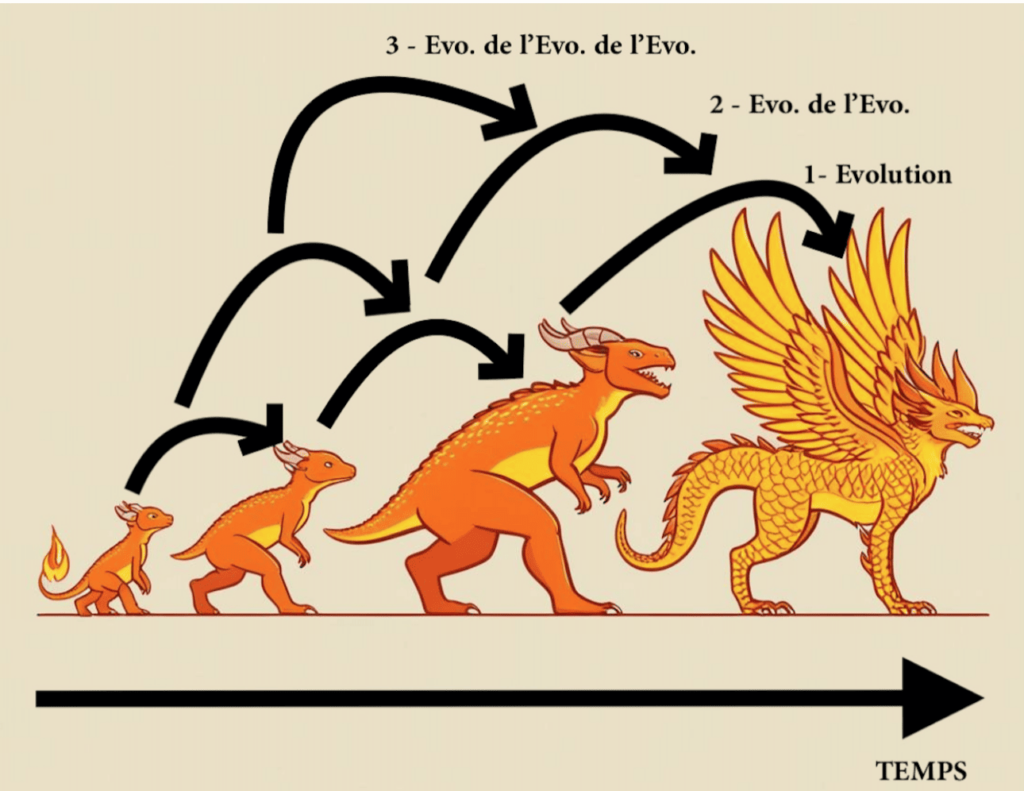
Fig.2 Représentation graphique du principe de variation jusqu’au troisième ordre.
Les lois qui décrivaient le système avant l’apparition d’une nouveauté ne suffisent plus car ce dernier a subi un changement fonctionnel irréversible.
Petit excursus mathématique
Nous montrons maintenant avec un petit exemple les difficultés mathématiques rencontrées dans la description de ces phénomènes. Tout lecteur effrayé par les mathématiques peut s’épargner toute souffrance en passant librement à la section suivante.
L'inaccessibilité des lois de l'évolution
Prenons l’évolution d’un ensemble de lois Ω qui régulent la dynamique temporelle d’un certain système. L’introduction d’une nouveauté dans les lois Ω implique une variation fonctionnelle imprévisible 𝑓1 de Ω à un certain moment de son histoire. Nous appelons ce changement 𝑓1(Ω). En nous inspirant de la Fig. (2), les nouvelles lois seront elles-mêmes également soumises à un autre changement 𝑓2. En itérant ce raisonnement, on obtient pour la n-ième variation une expression du type :
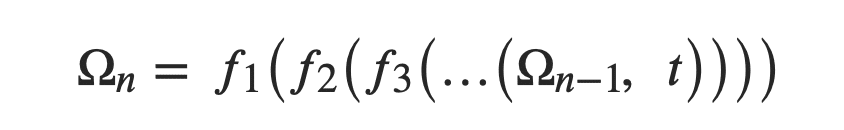
Ainsi écrite, l’évolution du système pourrait donc être interprétée comme le résultat d’une hiérarchie de fonctions 𝑓𝑖 définissant la dynamique de l’évolution des lois.
Cependant, on peut montrer [1] que le seul cas dans lequel on trouve l’EO est celui où, à tout moment, une nouvelle fonction 𝑓 peut apparaître dans n’importe quel ordre hiérarchique. Sous ces hypothèses, la variation est donc incalculable et aucune prédiction n’est possible. En résumé, si une dynamique suit l’EO, alors elle n’est pas descriptible par un ensemble énumérable d’équations.
La notion de créativité
Mais alors, est-il possible de prédire l’arrivée d’une nouveauté si celle-ci est imprévisible ?
En d’autres termes, quel est le minimum que l’on puisse dire sur ce dont on ne peut pas parler ? Existe-t-il un moyen de prédire au moins l’arrivée d’une nouveauté, sans pour autant la détailler ? Peut-on déterminer quand un système est capable d’évoluer ouvertement, sans nécessairement préciser dans quelle direction il évoluera ?
Pour répondre à ces questions, nous utiliserons la *complexité de Kolmogorov*, ou complexité algorithmique. Cette quantité, définie par le mathématicien russe Andreï Kolmogorov, correspond à la taille du plus petit algorithme possible capable d’engendrer un objet.
Dans le cas de l’étude d’un système particulier, nous pouvons approcher cette complexité en considérant la taille du plus petit algorithme connu.
Évoluer, c'est booster sa complexité
Dans le cas des systèmes vivants, on peut parler de complexité de la description des objets spécifiques, qui, après l’apparition d’une nouveauté fonctionnelle, doit augmenter. Toutefois, une série d’apparitions de nouveautés a un impact plus important qu’une simple série d’évènements aléatoires. C’est à partir de cette hypothèse que des développements théoriques récents [2] soutiennent que l’EO se retrouve dans des systèmes où la complexité K augmente dans le temps t plus qu’une chaîne aléatoire. La complexité d’une chaîne aléatoire augmentant linéairement dans le temps, on peut dire que la croissance de la complexité dans le cas de l’EO augmente au moins de manière super-linéaire. En termes mathématiques [2] :
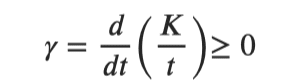
Nous appellerons 𝛾 créativité. Un système créatif est donc un système capable de générer des nouveautés. En d’autres termes, on peut dire que l’EO engendre des changements qui suivent une logique de dynamique historique comme l’est la sélection naturelle et qui sont donc plus qu’un simple processus aléatoire.
D’autres façons d’estimer la complexité d’un objet peuvent être développées ad hoc pour chaque système, comme c’est le cas, par exemple, de la théorie de l’Assemblage [3,4] récemment élaborée pour les systèmes chimiques. Cette théorie propose d’évaluer la complexité d’une molécule chimique en utilisant le nombre de réactions nécessaires pour la synthétiser.
Pour ouvrir... il faut clôturer !
En revanche, l’évolution ouverte ne peut opérer sans certaines conditions.
Par exemple, une espèce qui évolue est aussi une espèce qui possède une histoire d’évolution. Cela signifie que l’évolution ouverte correspond à la variation ultérieure d’une espèce dont les lois du système avaient déjà subi d’autres variations.
L’apparition d’une nouvelle variation est une propriété émergente. C’est comme si elle représentait un « talent » créatif caché.
Pour qu’il y ait émergence, il est essentiel que les constituants du système s’organisent. Ils doivent sélectionner les processus les mieux adaptés au contexte et à l’histoire spécifiques dans lesquels ils s’inscrivent. Darwin appelle cela sélection.
La notion de clôture
Dans un système à multi-agents, c’est-à-dire composé de plusieurs individus, l’évolution ouverte est liée causalement à la notion de *clôture* [4,5]. Cette notion suggère une interdépendance et une inter-activation des composants sur un certain intervalle de temps.
L’existence de certains constituants du système devient alors essentielle à la survie des autres. Cela crée, à long terme, un contexte dans lequel des objets spécifiques sont sélectionnés. Ces objets deviennent progressivement de plus en plus complexes.
Un exemple de clôture se trouve dans les systèmes de réactions chimiques, à la base de tout système vivant et, plus largement, de la vie. Prenons un système de réactions catalytiques, où la vitesse des réactions augmente en présence d’une molécule appelée catalyseur. Dans ce cas, on peut démontrer l’émergence d’une évolution ouverte lorsque les réactions s’auto-organisent pour former un groupe autocatalytique. Ce groupe est un ensemble de réactions catalytiques qui produisent leurs propres catalyseurs [4].
En résumé, plus les composants du système s’organisent selon le principe de la clôture, plus les forces sélectives s’intensifient. Dans ce cadre, les espèces ayant de meilleures capacités d’adaptation auront une probabilité accrue de générer des nouveautés, et donc de survivre.
Applications
Des exemples d’EO de notre quotidien sont par exemple l’évolution des langues, de la musique, ainsi qu’un nombre incalculable de phénomènes culturels. L’étude des méthodes permettant de stimuler la créativité d’un système est à la base de différents types de recherche fondamentale, car ce genre de phénomènes fait partie intégrante de notre vie.
Des applications omniprésentes
L’intelligence artificielle est l’un des domaines d’application principaux, surtout depuis ‘l’introduction de l’IA générative. Dans le domaine de l’IA, l’idée est de pousser cette technologie vers la génération autonome de nouveautés [6-7]. En effet, contrôler la créativité d’un système sera de plus en plus important dans des domaines comme la cryptographie ou la défense, où prédire et éventuellement contrôler la créativité peut compenser l’absence d’informations spécifiques des évènements futurs. Même l’industrie vidéoludique a récemment commencé à développer des jeux créatifs capables non seulement de générer de nouvelles quêtes secondaires en totale autonomie, mais aussi de faire évoluer le monde du jeu avec ses personnages. Cette fonctionnalité pousserait le moteur du jeu à générer d’autres jeux qui augmentent la complexité et la longévité de l’expérience principale [e.g. Minecraft, Elder Scrolls 6, GTA VI, etc.].
Dans la recherche fondamentale, les scientifiques s’inspirent de la théorie de l’EO pour essayer de développer un cadre mathématique formel capable de mieux décrire la vie et son évolution. Toutefois, la vie et son évolution sont encore aujourd’hui des phénomènes inexplicables. Même si de grands scientifiques ont essayé de leur donner un sens (cf. [8]), les lois de la vie semblent encore aujourd’hui échapper astucieusement à notre compréhension.
Conclusions
Grâce à cet article, nous avons découvert la notion d’évolution ouverte, un processus d’introduction de nouveautés fonctionnelles typique des systèmes vivants. Ces nouveautés sont, par nature, imprédictibles, ce qui rend leur étude très difficile. Nous avons vu qu’il est possible d’évaluer la créativité d’un système afin de développer des méthodes qui déterminent le moment où un système évolue ouvertement. Cependant, l’OE n’est pas un phénomène qui émerge gratuitement. C’est pour cette raison que ce type d’évolution apparaît dans des systèmes hautement dépendants de leur histoire et qui arrivent à mieux s’adapter aux changements. Celui qui arrive à s’adapter aux forces sélectives étant également celui qui est avantagé par la sélection, ce cadre théorique est très bien représenté par la notion de clôture.
Morale de l'histoire
En fin de compte, nous pouvons dire que la clef pour accéder à l’évolution ouverte réside dans un compromis qui semble aussi contradictoire qu’il devrait être évident pour ceux qui m’ont suivi jusqu’ici : si l’on veut que notre système évolue ouvertement, il faut d’abord qu’il soit clos !
Si vous souhaitez en savoir plus ou si ces arguments ont suscité votre intérêt, et que vous envisagez d’intégrer l’un de nos experts à votre équipe, n’hésitez pas à nous contacter ici. Nous serons ravis de vous fournir davantage de détails et de discuter de solutions personnalisées adaptées à vos besoins. Nos spécialistes sont à votre disposition pour explorer ensemble des opportunités de collaboration et garantir des résultats d’excellence.
Bibliographie
[1] Maël Montevil, Matteo Mossio, Arnaud Pocheville, and Giuseppe Longo, “Theoretical principles for biology: Variation. Progress in Biophysics and Molecular Biology”, 122(1):36–50, October 2016.
[2] Bernat Corominas-Murtra, Luıs F. Seoane, and Ricard Sole, “Zipf’s Law, unbounded complexity and open-ended evolution”, Journal of The Royal Society Interface, 15(149):20180395, December 2018.
[3] Abhishek Sharma, Daniel Czégel, Michael Lachmann, Christopher P. Kempes, Sara I. Walker, and Leroy Cronin, “Assembly theory explains and quantifies selection and evolution”, Nature, 622(7982):321–328, October 2023.
[4] Marco Faggian, “Evidence of causality between Closure and Open-Ended Evolution in the Kauffman model”, bioRxiv, Novembre 2024
[5] Alvaro Moreno and Matteo Mossio. Biological autonomy: a philosophical and theoretical enquiry, volume 12. Springer, 2015.
[6] Tijn Van der Zant, Matthijs Kouw, Lambert Schomaker, “Generative Artificial Intelligence”, Springer Nature
[7] “Open-Ended Intelligence”, 9th International Conference, AGI 2016, New York, NY, USA, July 16-19, 2016, Proceedings
[8] Erwin Schrödinger, “What is life ?”

Marco FAGGIAN
Consultant Data Scientist





